Knowing how fast your algorithm runs is extremely important. Often times, you will get asked to determine your algorithm performance in a big-O sense during interview. You will be expected to know how to calculate the time and space complexity of your code, sometimes you even need to explain how you get there. In some cases, it can be pretty tricky to get it right. In this article, I am going to show you guys how to do things right.
In most of the cases, you are going to see these kind of Big-O running time in your code.
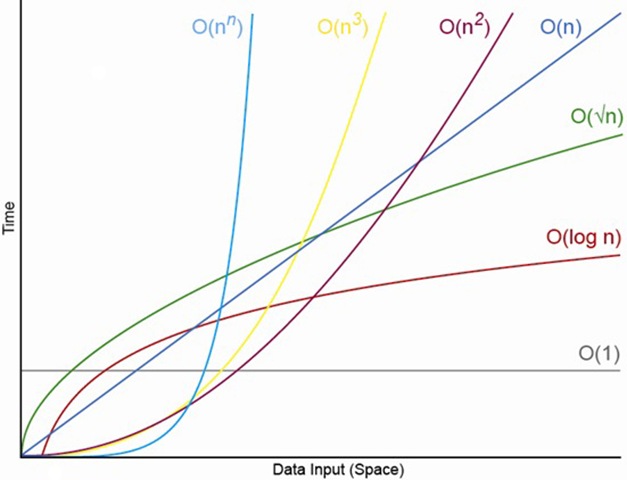
Diagram above is from Objective-C Collections by NSScreencast
Let me give you example of how the code would look like for each running time in the diagram.
// Time complexity: O(1)
// Space complexity: O(1)
int x = 15;
x += 6;
System.out.print(x); // should print 21source code hosted on GitHub
As we all know, math operators like +, -, *, / computes in constant time. Since the code does nothing but addition and printing, it indeed runs in constant time.
Next,
// Time complexity: O(log(n))
// Space complexity: O(1)
public static int binarySearch(int [] arr, int target) {
int low = 0, high = arr.length - 1;
while(low <= high) {
int mid = low + ((high - low) / 2);
if(arr[mid] == target) return mid;
if(arr[mid] < target) low = mid + 1;
else high = mid - 1;
}
return -(low + 1);
}
public static void main(String[] args) {
int [] arr = new int[]{2, 3, 5, 7, 9, 19, 25};
System.out.println(binarySearch(arr, 2) == 0); // true
System.out.println(binarySearch(arr, 19) == 5); // true
System.out.println(binarySearch(arr, 1) == -1); // true
System.out.println(binarySearch(arr, 20) == -7); // true
System.out.println(binarySearch(arr, 18) == -6); // true
}source code hosted on GitHub
Just like any other binary search, this code runs in logarithmic time. Say we are given an array that looks something like [2, 3, 5, 7, 9, 19, 25], we start from the midpoint (where the 7 is) and try to look for our target (say, 2). Since it was already sorted, we know that our target is less than where the midpoint value is. As a result, the answer has to be on the left side if it exist at all (or on the right side if our target is larger than the midpoint value). We then keep doing that. Eventually, we will either find our target number or find the index where the target number should be (to insert in order to say sorted). As you can see in each iteration(s), we are essentially cutting arrays into half and check to see if our target number is on the left or on the right side. Hence, we are only doing logarithmic works. Please head over to this awesome Stack Overflow threads to learn more in depths.
Next,
// Time complexity: O(sqrt(n))
// Space complexity: O(1)
public static boolean isPrime(int n) {
boolean isPrime = true;
for(int i = 2; Math.sqrt(n) > i && isPrime; i++) {
if(n % i == 0) isPrime = false;
}
return isPrime;
}
public static void main(String[] args) {
System.out.println(isPrime(2) == true);
System.out.println(isPrime(5) == true);
System.out.println(isPrime(7) == true);
System.out.println(isPrime(12) == false);
System.out.println(isPrime(20) == false);
}source code hosted on GitHub
As you can see, in the isPrime method, our for loop starts iteration from 2 and will only go up to the square root of n. Hence, it is only doing square root of n works where n is the number to be checked. The reason we only need to computes up to square root of n is because
If a number n is not a prime, it can be factored into two factors a and b:
n = a * b
If both a and b were greater than the square root of n, a * b would be greater than n. So at least one of those factors must be less than or equal to the square root of n, and to check if n is prime, we only need to test for factors less than or equal to the square root.
answered by Sven Marnach in this Stack Overflow threads: Why do we check up to the square root of a prime number to determine if it is prime?
Next,
// Time complexity: O(n)
// Space complexity: O(1)
public static void printArray(int [] arr) {
for(int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
public static void main(String[] args) {
int [] arr = new int[]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
printArray(arr);
}source code hosted on GitHub
Given an array of size n, we have a for loop that go through each and every one of the elements in the array. In each iteration, we are simply printing the values in the array. As a result, our code should runs in linear time.
How about this code?
// Time complexity: O(n)
// Space complexity: O(1)
public static void printArray(int [] arr) {
for(int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
public static void main(String[] args) {
int [] arr = new int[]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
printArray(arr);
printArray(arr);
printArray(arr);
}source code hosted on GitHub
The biggest differences between this code and the code above is that it consists of 3 for loops. Since each for loop runs in linear time, three of them simply makes them 3 * n, in big-O sense, it will still concluded as O(n) as 3 is a constant when n gets large!
Next,
// Time complexity: O(n^2)
// Space complexity: O(1)
public static void print2DArray(int [][] m) {
for(int i = 0; i < m.length; i++) {
for(int j = 0; j < m[0].length; j++) {
System.out.print(m[i][j] + ",");
}
System.out.println();
}
}
public static void main(String[] args) {
int [][] m = new int[3][3];
m[0][0] = 1;
m[0][1] = 2;
m[0][2] = 3;
m[1][0] = 4;
m[1][1] = 5;
m[1][2] = 6;
m[2][0] = 7;
m[2][1] = 8;
m[2][2] = 9;
print2DArray(m);
}source code hosted on GitHub
Given a 2D array, we are going through each and every one of the rows and cols in the matrix. In each iteration, we are simply printing which takes constant time. Overall, we are doing quadratic works.
How about this code?
// Time complexity: O(n^2)
// Space complexity: O(1)
public static void print2DArray(int [][] m) {
for(int i = 0; i < m.length; i++) {
for(int j = 0; j < m[0].length; j++) {
for(int k = 0; k <= 10; k++) {
System.out.print(m[i][j] + ",");
}
}
System.out.println();
}
}
public static void main(String[] args) {
int [][] m = new int[3][3];
m[0][0] = 1;
m[0][1] = 2;
m[0][2] = 3;
m[1][0] = 4;
m[1][1] = 5;
m[1][2] = 6;
m[2][0] = 7;
m[2][1] = 8;
m[2][2] = 9;
print2DArray(m);
}source code hosted on GitHub
We have added another for loop within the nested for loop that we already have. However, instead of going from zero up to the matrix size, we go from zero up to the number of 10. Will that increase our time complexity? The correct answer is no. Since our for loop runs up to a constant number of 10 and does not grow as n grows, hence, the time complexity of this code is still a solid O(n^2). It is important to discard things that does not grow as n grows since they will become irrelevant when you are trying to determine your code run time in big-O sense.
Next,
// Time complexity: O(n^3)
// Space complexity: O(1)
public static void print2DArray(int [][] m) {
for(int i = 0; i < m.length; i++) {
for(int j = 0; j < m[0].length; j++) {
for(int k = 0; k < m[0].length; k++) {
System.out.print(m[i][j] + ",");
}
}
System.out.println();
}
}
public static void main(String[] args) {
int [][] m = new int[3][3];
m[0][0] = 1;
m[0][1] = 2;
m[0][2] = 3;
m[1][0] = 4;
m[1][1] = 5;
m[1][2] = 6;
m[2][0] = 7;
m[2][1] = 8;
m[2][2] = 9;
print2DArray(m);
}source code hosted on GitHub
We have nested of three for loops in the print2DArray method, they all go up to the size of the matrix which makes this code a cubic time or O(n * n * n).
Before we talk about how we can get time complexity of O(n^n), let’s perhaps talk about how you can get O(4^n) first. Say, you are given this question,
Given a list of float numbers, insert “+”, “-”, “*” or “/” between each consecutive pair of numbers to find the maximum value you can get. For simplicity, assume that all operators are of equal precedence order and evaluation happens from left to right. For example:
Given a list of number, [1, 12, 3], the maximum value you can get is 39 if you do 1 + 12 * 3.
To visualize it, here is the tree that I drew,
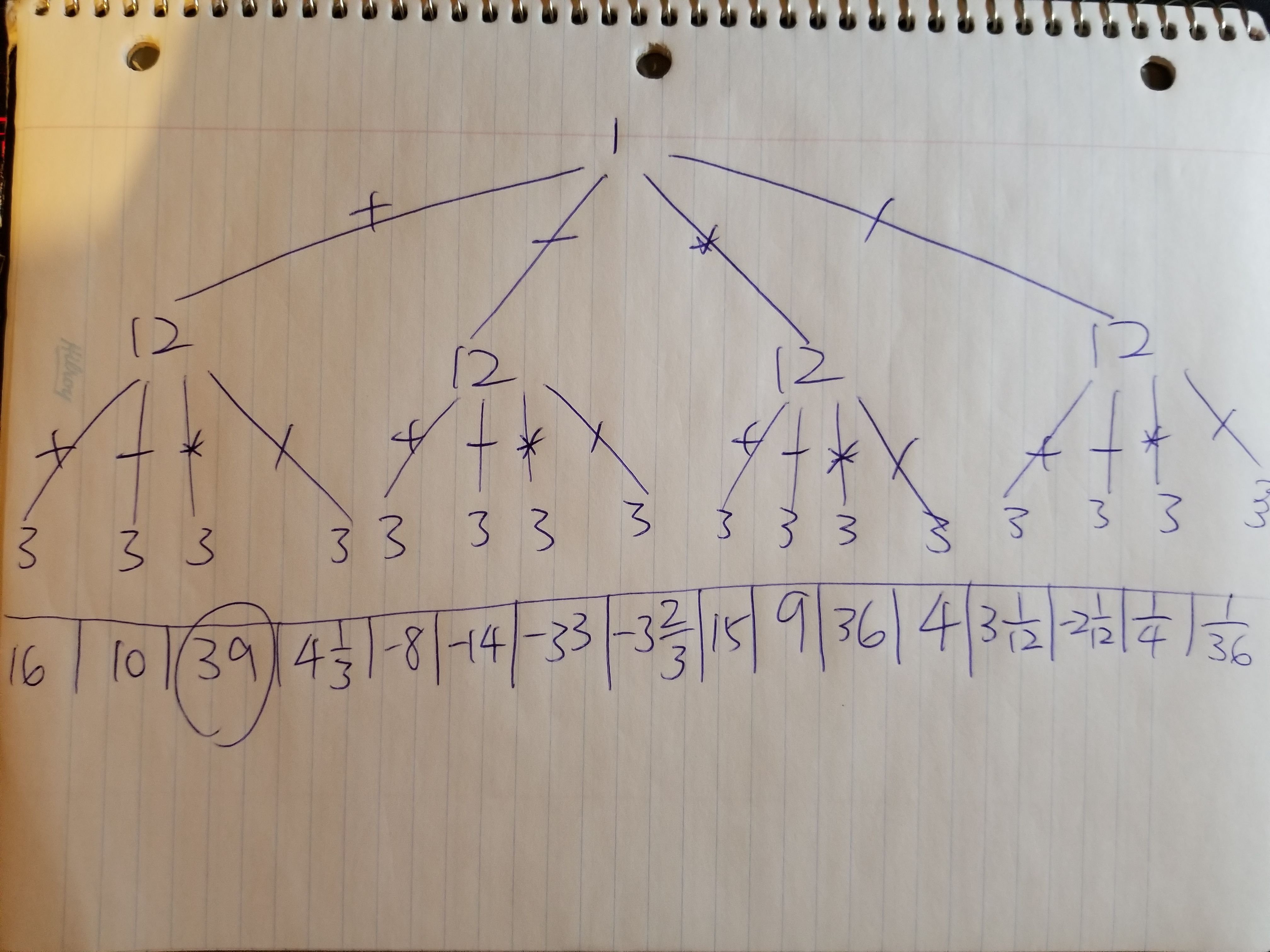
As you can see all the paths, 1 + 12 * 3 has the largest value out of all of them which is the answer. Normally, each tree node in a binary tree has 2 branches to grow out. For the tree that I drew, each tree node can grow into 4 branches. In the first level, it has 1 tree nodes. In the second level, it has 4 tree nodes. In the third level, it has 16 tree nodes. Guess how many tree nodes in the forth level? the answer is 64. You might wonder how we got the answer, it is simple. We simply do 4**level. 4**0 is 1, 4**1 is 4, 4**2 is 16, and 4**3 is 64. As you can see, this exactly matched the number of tree nodes in each level of the tree that we drew. We can then generalized the total number of tree nodes to 4**n where n is the number of levels or number of items in the list which is also the run time of the algorithm.
Here is what the code might looks like,
// Time complexity: O(4^n)
// Space complexity: O(1)
public static void getMaxAnswer(double res, int [] arr, int index) {
if(index == arr.length) {
System.out.println(res);
} else {
getMaxAnswer(res + arr[index], arr, index + 1);
getMaxAnswer(res - arr[index], arr, index + 1);
getMaxAnswer(res * arr[index], arr, index + 1);
getMaxAnswer(res / arr[index], arr, index + 1);
}
}
public static void main(String[] args) {
int [] arr = new int[]{1, 12, 3};
getMaxAnswer(arr[0] * 1.0, arr, 1);
}source code hosted on GitHub
As we explained earlier, this code has the running time of O(4^n).
With this in mind, you should be able to create a code that does O(n^n), instead of limiting our operator to only four of them (“+”, “-”, “*” or “/”), we simply have n number of operators, then the code running time would be O(n^n). Why not leave what the code might look like for run time of O(n^n) in the comments below?
Wrapping Up
Hopefully you enjoyed this tutorial about how to calculate the time complexity of an algorithm. Let me know if this helps you. Thank you for reading!
Resources
I’ll try to keep this list current and up to date. If you know of a great resource you’d like to share or notice a broken link, please let us know.
Getting started
Author
PoAn (Baron) Chen
Software Engineer at Microsoft. Graduated from @uvic. Previously worked at @illumina, @ACDSee, @AEHelp and @AcePersonnel1. My words are my own.
Comments