Today, I am going to give a tutorial on how to solve the Fibonacci problem using Dynamic Programming in Java. Before we start to talk about Dynamic Programming. I would like to start briefly on what the Fibonacci problem is. If you already know the problem. Feel free to skip to the next section.

Fibonacci problem

According to Wikipedia, “Fibonacci number are the numbers in the following integer sequence, called the Fibonacci sequence, and characterized by the fact that every number after the first two is the sum of the two preceding ones”

For example: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55

In modern usage, the sequence is extended by one more initial item: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55

In any given sequence of Fn, it often represent as,
Fn = Fn-1 + Fn-2, with seed value of F1=1, F2=1 or F0=0, F1=1 depends on your first initial value.

These are the values at the nth of the Fibonacci sequence.

0 1 2 3 4 5 6 7 8 9 10
0 1 1 2 3 5 8 13 21 34 55

For example, at the 8th of Fibonacci sequence is 21.

Okay, now that we have Fibonacci problem covered. Let’s talk about Dynamic Programming and how it can be useful to us to solve this problem.

Dynamic Programming

The basic idea of Dynamic Programming is to save the result of the subproblem so that if we see it again in the future. We can simply use it instead of recomputing the value again. In the long run, it should save some or a lot of time which reduces the running time complexity of the problem. (which is what you should always try to do when doing competitive programming questions)

Let’s take the simple example of the Fibonacci numbers: finding the nth Fibonacci number defined by Fn = Fn-1 + Fn-2 and F0=0, F1=1

The easiest and obvious way of doing this is to use the recursion:

Recursion

  public int getFibonacciNumberRecursively(int n) {
    if(n == 0) return 0;
    if(n == 1) return 1;
    return getFibonacciNumberRecursively(n - 1) + getFibonacciNumberRecursively(n - 2);
  }

source code hosted on GitHub

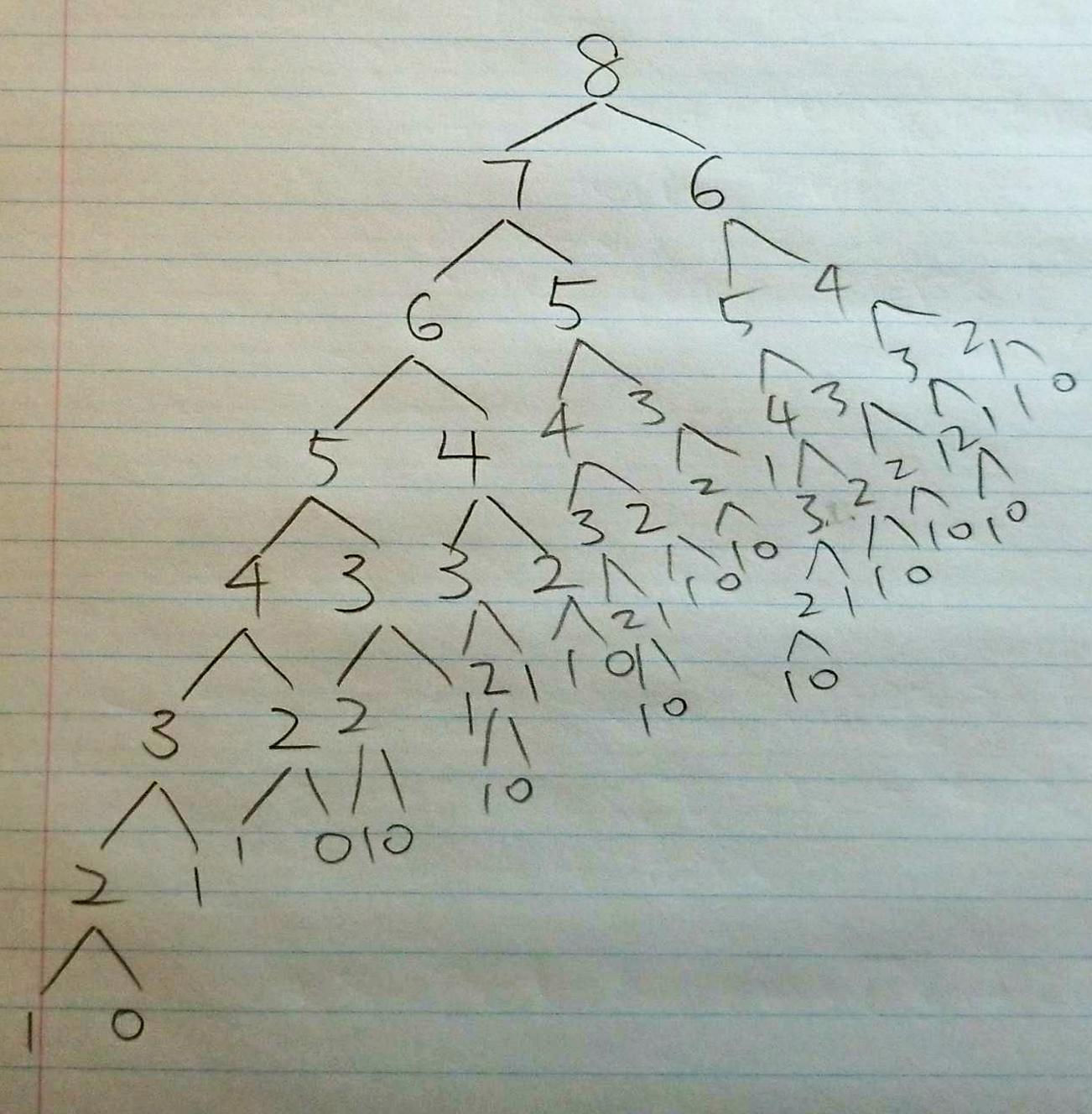
fibonacci number recursive tree diagram for 8

As you can see in the tree diagram, number 7 has been computed 1 time. Number 6 has been repeatly computed 2 times. Number 5 has been repeatly computed 3 times. Number 4 has been repeatly computed 5 times. Number 3 has been repeatly computed 8 times. The times grow as the number n gets larger. How can we stop doing that? (trying to recompute a fib(n) that we already did before)

Here is where the Dynamic Programming comes into play that will save us all.

Top Down - Memoization

When the recursion does a lot of unnecessary calculation, just like one above, an easy way to solve this is to cache the results. Whenever you are trying to computer a number say n. We first check if have done that before in our cache. If we did, simply return what was in the cache. Otherwise, try to compute the number. Once we get the number, we make sure to put the result to the cache for use in the future.

  public HashMap<Integer, Integer> hm = new HashMap<Integer, Integer>();
  public int getFibonacciNumberTopDown(int n) {
    if(hm.containsKey(n)) return hm.get(n);
    if(n == 0) return 0;
    if(n == 1) return 1;
    int nthValue = getFibonacciNumberTopDown(n - 1) + getFibonacciNumberTopDown(n - 2);
    hm.put(n, nthValue);
    return nthValue;
  }

source code hosted on GitHub

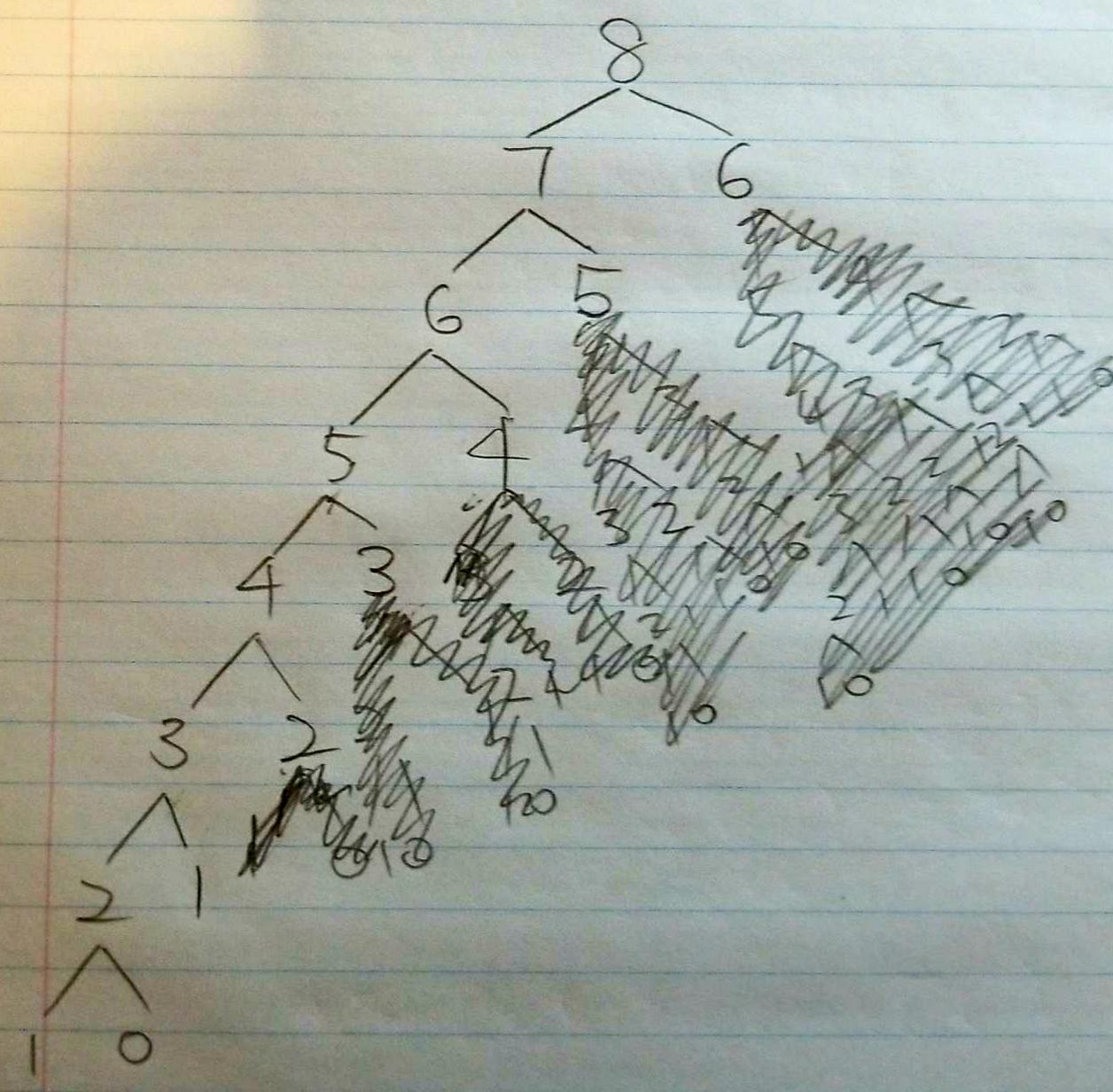
fibonacci number top down tree diagram for 8

By using the caching technique or Memoization, we have eliminate the needed to recomputed a lot of numbers as you can see in the tree diagram above. Hence, the running time should be improved tons. However, the space complexity of the problem just got increased to O(N) as we created a HashMap to store the results of the value. (acting as cache) However, this is still not perfect. As you can see, number 7 has been asked 1 time. Number 6 has been asked 2 times. Number 5 has been asked 2 times. Number 4 has been asked 2 times. Rest of the number got asked twice except 0. The next question is, is it possible that all the number will get computed/asked once and we get what we want at the end?

Yes, it is totally possible. Let’s try it.

Bottom Up

A better way to do this is to get rid of the recursion all-together by evaluating the results in the right order. Instead of top down, we are going for bottom up.

  public HashMap<Integer, Integer> hm = new HashMap<Integer, Integer>();
  public int getFibonacciNumberBottomUpWithCache(int n) {
    hm.put(0, 0);
    hm.put(1, 1);
    for(int i = 2; i <= n; i++) {
      hm.put(i, hm.get(i - 1) + hm.get(i - 2));
    }
    return hm.get(n);
  }

source code hosted on GitHub

Now that we are going with the right direction. Each number in the sequence ONLY gets touch once. Hence, the running time should get further improved here compared with the top down approach. However, the next question is, do we really need to save the results to the cache? and waste another O(N) space. The answer here is not really. We can use constant space and store the only necessary partial results along the way:

  public int getFibonacciNumberBottomUpWithoutCache(int n) {
    if (n == 0 || n == 1) return n;
    int fnMin2 = 0;
    int fnMin1 = 1;
    int sum = 0;
    for(int i = 2; i <= n; i++) {
      sum = fnMin1 + fnMin2;
      fnMin2 = fnMin1;
      fnMin1 = sum;
    }
    return sum;
  }

source code hosted on GitHub

Here, the runnning time for this approach should stay O(N) like above using the cache. However, we greatly reduced the space complexity from O(N) to O(1) constant space. Both running time and space complexity optimized.

Tada. You have done it using the Dynamic Programming way=)

Wrapping Up

This tutorial is largely based on a StackOverflow post by Tristan.

His idea of applying the Dynamic Programming is as follows:

Notes from his as well: Dynamic programming generally works for problems that have an inherent left to right order such as strings, trees or integer sequences. If the naive recursive algorithm does not compute the same subproblem multiple time, dynamic programming won’t help.

In case you want to run the live example, click the link here.

Hopefully this guide has help you to solve the Fibonacci problem using the Dynamic Programming. Thank you for reading!

Resources

I’ll try to keep this list current and up to date. If you know of a great resource you’d like to share or notice a broken link, please let us know.

Getting started